Series cuantitativas / Continuas

Histograma

Se usa para representar gráficamente variables continuas agrupadas en distribuciones de frecuencias. En el histograma cada una de las barras continuas corresponde a una de las clases de la distribución de frecuencias.

Para facilitar la interpretación, sólo se representa la distribución de frecuencias de una sola serie estadística. Si la distribución tiene más de una serie, es mejor usar el polígono de frecuencias, que sí permite representar más de una serie cuantitativa continua en el mismo gráfico.

La variable continua se coloca en el eje “X” y corresponde a los límites reales de la distribución de frecuencias. Su forma es similar a la del gráfico de barras verticales, pero como la variable es continua las barras se colocan juntas.

En este gráfico la comparación se hace con respecto a la longitud y al ancho o área de cada una de las barras; la longitud de las barras representa la frecuencia absoluta o relativa de la variable y el ancho corresponde al intervalo de las clases en que han sido agrupados los datos. Cuando todos los intervalos tienen el mismo tamaño todas las barras tienen el mismo ancho y la altura estará determinada por la frecuencia de cada una de las clases, como en el gráfico 22.

Gráfico 22: muestra la población económicamente activa (PEA), por intervalos iguales de edad de diez años, de 19 a 69 años. Se observa una mayor concentración de población en las edades de 19 a 49 años; a partir de la edad de 49 años empieza a disminuir la PEA, como es de esperar, porque los trabajadores al aumentar su edad empiezan a pensionarse.

Gráfico N°23: representa la población económicamente activa (PEA), por grupos de edad de 14 a 69 años, pero en intervalos de diferente tamaño. La distribución de la PEA muestra la misma tendencia que en el gráfico N°22.

En este gráfico por tener intervalos de edad de diferente tamaño, se ha calculado la densidad de frecuencia que se representa en el eje “Y”; las barras muestran, claramente, las distancias que se encuentran entre el límite superior y el inferior, por ejemplo la clase de 49,5 a 59,5 es el doble (10 años) de la clase de la clase de 24,5 a 29,5 (5 años).

Gráfico N°24: representa las tasas de fecundidad de la población femenina de 15 a 49 años, por intervalos iguales de edad de cinco años. Se observa que las tasas de fecundidad más altas se presentan en la población de 19 a 29 años, aunque las mujeres de 14 a 19 y de 29 a 34 años presentan tasas menores representan un grupo muy importante en el estudio de la fecundidad. A partir de los 34 años se produce un fuerte descenso en la fecundidad. Cuadro N°19.

Cuando los tamaños de los intervalos son diferentes se ajusta el área de la barra al tamaño del intervalo, para evitar que la figura represente áreas demasiado amplias a causa más del tamaño del intervalo que de la magnitud de frecuencia.

A continuación se presenta el cálculo de la densidad de frecuencia del gráfico N°23:

*Intervalo base es 5

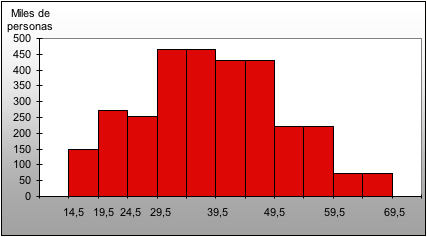
Si la frecuencia no se ajusta, se produce una distorsión visual de la imagen, porque el lector va a confundir la amplitud del área representada con la magnitud de la frecuencia, como se observa en el siguiente grafico que no tiene el ajuste de las frecuencias.

Este gráfico se elaboró con los mismos datos del gráfico Nº 23, a pesar de que sus intervalos tienen diferente tamaño no tiene el ajuste de las frecuencias, lo que produce que el lector observe un área mayor en las clase de 29,5 a 39,5 y de 39,5 a 49,5, pero esto ocurre porque el tamaño de estas clases tienen mayor amplitud y no porque sean mayores que la clase de 19.5 a 24,5 y de 24,5 a 29,5.

Si el tamaño del intervalo de cada una de las clases es el mismo, sólo se representan en el gráfico los valores de las clases y las frecuencias, como en los gráficos Nº 22 y 24. Si los intervalos de las clases tienen diferente tamaño, como en el gráfico N° 23, lo que se representa en el eje de las ordenadas es la densidad de la frecuencia.

¿Por qué se prefiere el histograma y no el gráfico de barras verticales para estos datos?

Cálculo de la densidad de la frecuencia

La densidad de la frecuencia se calcula con los siguientes pasos:

• Se determina el tamaño del intervalo.
• Se escoge un intervalo base o de referencia, que puede ser el más frecuente o un múltiplo de 5.
• Luego se divide: (Frecuencia absoluta de la clase i * Intervalo base) / Tamaño del intervalo de la clase i
• La densidad de frecuencia es la que se grafica en el eje de las ordenadas.

Normas de presentación

• Las barras están juntas porque representan una variable continua.
• En el eje de las abscisas, o eje “X”, se representa los valores de las clases que agrupan la variable de interés.
• En el eje de las ordenadas, o eje “Y”, se representa la frecuencia del número de observaciones de cada una de las clases, es decir, se coloca la frecuencia absoluta o relativa de las clases representadas.
• Las barras tienen como base el eje de las abscisas y su altura es directamente proporcional a la magnitud de la frecuencia correspondiente.
• Cuando las clases tienen tamaños diferentes de intervalo se debe calcular las frecuencias ajustadas o densidad de frecuencia. Esto con el propósito, de que la escala del eje de las abscisas represente apropiadamente la diferencia en la magnitud de las clases.
• La primera barra de la izquierda, debe estar separada del eje “Y” por una distancia equivalente al tamaño de una barra, o a la mitad de ésta. A menos que el primer intervalo se inicie en cero.

Diagrama cartesiano (PDF).